|
Занимательная математика
|
|
| Race | Дата: Пн, 04.12.17, 23:09 | Сообщение # 101 |

Просветленный  Сообщений: 459
| Vita, мои аплодисменты. Это безусловно решение)
Правда я подразумевал иное, но Ваше полностью удовлетворяет заданному условию, разве что не все вершины касаются сторон четырехугольника)Добавлено (04.12.2017, 23:09)
---------------------------------------------
|
| |
| |
| Vita | Дата: Вт, 05.12.17, 08:11 | Сообщение # 102 |
Гений  Сообщений: 1584
| Цитата Race (  ) Правда я подразумевал иное |
| |
| |
| Race | Дата: Вт, 05.12.17, 09:25 | Сообщение # 103 |

Просветленный  Сообщений: 459
| Цитата Vita (  ) Race, можете выложить авторское решение?
Для построения достаточно соединить середины сторон четырехугольника. Для любого четырехульника, не только выпуклого, получившийся четырехугольник будет паралелограммом, для выпуклого же, площадь параллелограмма будет равна половине площади исходного четырехугольника. Причем стороны получившегося параллелограмма, будут попарно равны половинам диагоналей и параллельны им же.
К сожалению, если я правильно помню, в школьной геометрии об этом факте не упоминается, я получил подобную информацию самостоятельно, уже в последствии подтвердил используя поиск гугла.
Доказывается элементарно, через подобие треугольников.
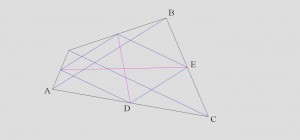
Рассмотрим треугольники ABC и DEC
Угол С у них общий, а так же AC=2DC и BC=2EC, соответственно треугольники подобны, с коеффициентом подобия равным 2.
Из этого в свою очередь следует что AВ ll DE, причем AВ=2DE.
Аналогичным образом рассматривая любой из маленьких треугольников образованный изначальным четырехугольником, с большим треугольником образованным диагональю и сторонами, доказываем что получившийся четырехугольник - параллелограмм, а так же что углы при вершинах параллелограмма ровняются углам при диагоналях заданного четырехугольника.
Ну дальше все просто:
Sчетырехугольника=[d1*d2*sin(d1^d2)]/2
Sпараллелограмма=(d1/2)*(d2/2)*sin(d1^d2)=[d1*d2*sin(d1^d2)]/4=Sчетырехугольника/2
Сообщение отредактировал Race - Вт, 05.12.17, 09:31 |
| |
| |
| Vita | Дата: Вт, 05.12.17, 12:47 | Сообщение # 104 |

Гений  Сообщений: 1584
| Спасибо, когда видишь готовое решение, всё кажется таким очевидным)
|
| |
| |
| Race | Дата: Вт, 05.12.17, 13:26 | Сообщение # 105 |

Просветленный  Сообщений: 459
| Цитата Vita (  ) Спасибо, когда видишь готовое решение, всё кажется таким очевидным) |
| |
| |
| Vita | Дата: Вт, 05.12.17, 19:24 | Сообщение # 106 |

Гений  Сообщений: 1584
| Доступно только для пользователей
Сообщение отредактировал Vita - Вт, 05.12.17, 19:43 |
| |
| |
| Race | Дата: Ср, 06.12.17, 09:20 | Сообщение # 107 |

Просветленный  Сообщений: 459
| Вы совершенно правы)
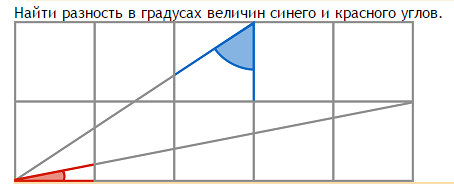
1. Решение, без сомнения Вы его практически нашли, получаем применив формулу для разницы аргументов тангенса, либо котангенса. Получаем 1.
2. Решение, Вы так же нашли, но тут предлагаю Вам доделать самостоятельно. Рассмотрите Ваш рисунок с зеленым треугольником. Это уже готовое решение, без применения тригонометрических формул.
|
| |
| |
| Vita | Дата: Ср, 06.12.17, 12:27 | Сообщение # 108 |

Гений  Сообщений: 1584
| Race, да рассматривала уже.Понимаю что он прямоугольный, но как это увидеть, не знаю. Достроить квадрат?
Сообщение отредактировал Vita - Ср, 06.12.17, 12:30 |
| |
| |
| Race | Дата: Ср, 06.12.17, 12:46 | Сообщение # 109 |

Просветленный  Сообщений: 459
| Vita, нет) Достаточно рассмотреть фиолетовые прямоугольники, которые есть на Вашем чертеже 
Сообщение отредактировал Race - Ср, 06.12.17, 12:47 |
| |
| |
| zhekas | Дата: Ср, 06.12.17, 15:14 | Сообщение # 110 |

Гуру  Сообщений: 166
Совы: 6 
| Цитата Vita (  ) Понимаю что он прямоугольный, но как это увидеть, не знаю
Левая часть верхнего угла, является дополнением до прямого для правой части верхнего угла
|
| |
| |
























