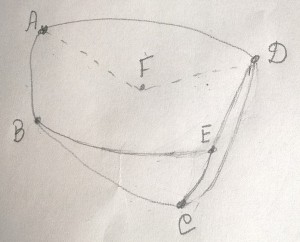
nebo, ну, видимо, например, так это должно выглядеть. Черное это на самом деле треугольники.
Добавлено (08.04.2018, 16:42)
---------------------------------------------
А может и не так. Потому что у меня по 2 грани ложатся на одну.
Цитата Kreativshik
Например вектор (1,6,9,5,1) определяет R(3,1,1) и R(2,3,0).
мне кажется, здесь наводка. Превращаем 1 четырехугольник в треугольник, другой в пятиугольник. Но на практике вычертить у меня не получается. Кроме прочего, мешает непонимание, что происходит когда вершина ложится на ребро, становится ли ребро 2 ребрами или остается 1.