|
Треугольники
|
|
|
| LonelyLeo | Дата: Чт, 21.08.14, 16:43 | Сообщение # 2 |

Мудрец  Сообщений: 604
Совы: 9 
|  Больше ничего... Больше ничего...
|
| |
| |
| Texnuk1984 | Дата: Пт, 16.01.15, 09:43 | Сообщение # 3 |

Гуру  Сообщений: 155
Совы: 1 
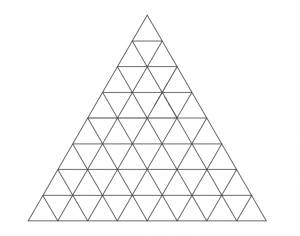
| Для этого рисунка: количество маленьких треугольников в основании большого n = 8,
сумма всех треугольников S = 92.
Если n = 1000, то S = 1499500.
|
| |
| |
| Texnuk1984 | Дата: Пт, 16.01.15, 11:10 | Сообщение # 4 |

Гуру  Сообщений: 155
Совы: 1 
| Сходил на свежий воздух, попил чайку и .....
Извините, я ошибся, - их там больше 
|
| |
| |
|
| erudite-man | Дата: Пт, 16.01.15, 16:02 | Сообщение # 6 |

Модератор
Сообщений: 1378
| Ну, вот смотри, треугольников второго порядка (см. рисунок) в первом ряду один, во втором - два и т. д. Собственно говоря, число таких треугольников равно сумме ряда 1+2+3+4+...+n.
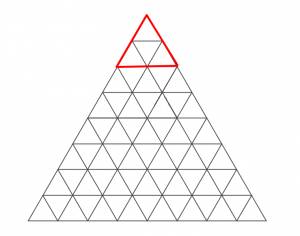
С треугольниками порядка три (см. рисунок), четыре и т. д., то же самое.
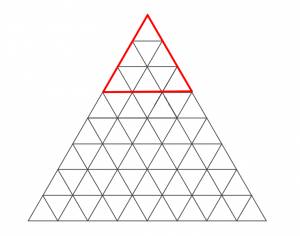
Треугольников порядка один, в первом ряду - один, во втором - три, в третьем - пять и т. д. Т. е. сумма таких треугольников равна 1+3+5+7+...
Советую познакомится с:
Треугольное число
Квадратное число
Задавайте вопросы, если что-то непонятно.
|
| |
| |
| Texnuk1984 | Дата: Вт, 20.01.15, 09:53 | Сообщение # 7 |

Гуру  Сообщений: 155
Совы: 1 
| n a1=n*n a2 a3 a4 a5 a6 a7 a8 a998 a999 a1000 S
1 1 1
2 4 1 5
3 9 3 1 13
4 16 6 3 1 26
5 25 10 6 3 1 45
6 36 15 10 6 3 1 71
7 39 21 15 10 6 3 1 105
8 64 28 21 15 10 6 3 1 148
998 996004 1
999 998001 997003 3 1
1000 1000000 999001 997003 6 3 1 500001499
n - порядок большого треугольника
ai - порядок маленьких треугольников входящих в большой
a(n) = a(1)+d*(n-1)
d=n
для a2:
A(998)=1+999*(999-1)=997003
A(999)=1+1000*(1000-1)=999001
для n=1000 от a2 до a1000
S(n)=(a1+an)*n/2
для a1000.........a2:
Только в формуле S(n) n=999, а не 1000,
т. к. для a1 S=1000000 — уже известно
S(1000)=(1+999001)*999/2=499001499
S(1000)(общее)=1000000+499001499=500001499
С большими числами я явно накосячил, т.к. формулы суммы для некоторых
значений "n" дает нецелое число.
Но смысл, мне кажется, чтобы посчитать сумму значений в нижнем ряду
таблицы справа налево от a1000 до a2, где значение увеличивается
каждый раз на единицу больше, чем в предыдущий, т.е. разность
арифм. прогресси d(i) = d(i-1) + 1. И к этому добавить a1 = 1000000
|
| |
| |
| Texnuk1984 | Дата: Вт, 20.01.15, 10:01 | Сообщение # 8 |

Гуру  Сообщений: 155
Совы: 1 
| n-----a1=n*n---- a2 ----a3- a4- a5- a6- a7- a8- a998- a999- a1000--------------- S
1----------1-------------------------------------------------------------------- 1
2----------4----- 1------------------------------------------------------------- 5
3----------9----- 3----- 1 -----------------------------------------------------13
4-------- 16----- 6----- 3-- 1 -------------------------------------------------26
5-------- 25 ----10----- 6-- 3-- 1--------------------------------------------- 45
6-------- 36---- 15---- 10-- 6-- 3-- 1----------------------------------------- 71
7-------- 39---- 21---- 15- 10-- 6-- 3-- 1------------------------------------ 105
8-------- 64---- 28---- 21- 15- 10-- 6-- 3-- 1-------------------------------- 148
998 --996004-------------------------------------- 1
999 --998001 997003------------------------------- 3---- 1
1000 1000000 999001 997003 ------------------------6---- 3--- 1--------- 500001499
|
| |
| |
| erudite-man | Дата: Вт, 20.01.15, 15:41 | Сообщение # 9 |

Модератор
Сообщений: 1378
| Честно говоря, я решал эту задачу немного по-другому. Если вы решите её другим способом, это будет более чем похвально, но, по правде говоря, я не совсем понимаю, что Вы делаете...
|
| |
| |
| nebo | Дата: Вт, 20.01.15, 16:59 | Сообщение # 10 |

Высший разум  Сообщений: 3639
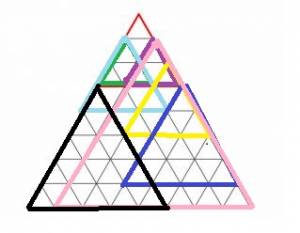
| erudite-man, ты пишешь
Цитата найдите количество треугольников
и тогда вопрос, а вот эти треугольники, которые у меня на рисунке цветные (конечно, не все,
их таких много), учитывать?
|
| |
| |















 Больше ничего...
Больше ничего...













