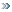Цитата nebo (
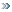
)
конечно, вот это
Цитата
последовательность ψ это коэффициенты генератрисы следующей функции с одной переменной (λ) λ4/((1-λ2)•(1-λ)3)
для меня подобно китайской грамоте
Ну давайте подробнее расскажу.
Разложение функции λ4/((1-λ2)•(1-λ)3) в ряд Тейлора в точке 0 , выглядит так
λ4+3λ5+7λ7+13λ8+22λ9...
коффециенты которого образуют последовательность ω:
0,0,0,1,3,7,13,22,34...
которая является смещённым аналогом ψ(пост#18),поэтому можно записать равенство (1):
ψn=ωn+3
А учитывая, что Цитата
количество треугольников, которое требуют найти условия данной задачи, в зависимости от количества частей на которые разделена сторона большого треугольника, образует последовательность (f):
δ1,δ2+ψ1,δ3+ψ2,δ4+ψ3
можно записать
fn=δn+ωn+2
Глядя на функцию для которой я представил разложение в ряд Тейлора и вспоминая о биноме Ньютона, несложно определить явную формулу для нахождения n-го элемента последовательности ω:
ωn=(3•cos(π•n)+4n3-18n2+20n-3)/48
Формула для нахождения n-го элемента последовательности δ:
δn=(n3+3n2+2n)/6
Учитывая (1) находим явную формулу для нахождения n-го элемента последовательности f:
fn=((n3+3n2+2n)/6)+((3•cos(π•(n+2))+4•(n+2)3-18•(n+2)2+20•(n+2)-3)/48)=(4n3+10n2+4n-1+cos(π•n))/16