|
Еще одна задача на построение.
|
|
| Race | Дата: Вт, 29.11.16, 12:05 | Сообщение # 1 |

Просветленный  Сообщений: 459
| На ЕГЭ встречаются геометрические задачи на построение.
То есть, школьник выпускник, должен обладать хотя бы минимальными познаниями в этой области. В то же самое время, практически нигде не дают необходимого опыта в рамках школьной программы.
Дано:
На плоскости был построен угол. После чего вершину угла (т. А) стерли,достраивать вершину угла запрещается.
Построить:
1. Биссектрису угла.
2. Для произвольной точки В, расположенной внутри угла, построить часть отрезка АВ.
Для тех кто справится с школьным уровнем, сделаем задачу №2 немного интересней:
2.1. Для произвольной точки В построить часть отрезка АВ. Разрешается использовать только линейку. Циркуль, угольник, транспортир запрещены.
Сообщение отредактировал erudite-man - Чт, 08.06.17, 21:45 |
| |
| |
| Ира | Дата: Вс, 19.02.17, 21:16 | Сообщение # 2 |

Гуру  Сообщений: 260
Совы: 6 
| Первая и вторая задачи не слишком сложные.
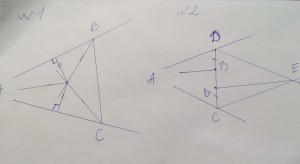
1.На сторонах угла А возьмем произвольные точки В и С, соединим их отрезком, построим биссектрисы углов АВС и АСВ, тем самым определим точку пересечения биссектрис тр-ка АВС, проведем из нее перпендикуляры к прямым АВ и АС и построим биссектрису угла между этими перпендикулярами.Искомая биссектриса лежит на этой же прямой.
2.Через т. В проведем прямую, пересекающую стороны угла А, получим точки Д и С. Проведем через них прямые, параллельные АС и АД соответственно, получим т. Е. От С отложим отрезок CB1 равный ДВ и соединим B1 с Е. Искомая прямая ВА будет параллельна B1E.
 Добавлено (19.02.2017, 21:16)
---------------------------------------------
А вот третья задача ставит меня в тупик. Ведь в задачах на построение линейка служит только для построения прямой через две точки...
Сообщение отредактировал Ира - Вс, 19.02.17, 21:13 |
| |
| |
| Race | Дата: Пт, 24.02.17, 12:26 | Сообщение # 3 |

Просветленный  Сообщений: 459
| Цитата Ира (  ) 1.На сторонах угла А возьмем произвольные точки В и С, соединим их отрезком, построим биссектрисы углов АВС и АСВ, тем самым определим точку пересечения биссектрис тр-ка АВС, проведем из нее перпендикуляры к прямым АВ и АС и построим биссектрису угла между этими перпендикулярами.Искомая биссектриса лежит на этой же прямой.
Более простым вариантом будет:
1. Биссектрисы треугольника пересекаются в одной точке, а значит, после построение биссектрис АВС и АСВ, берем на сторонах угла еще две произвольные точки В1 и С1 и производим с ними те же самые манипуляции.
2. Соединяем 2 полученные точки пересечения биссектрис. Полученный отрезок будет принадлежать биссектрисе угла
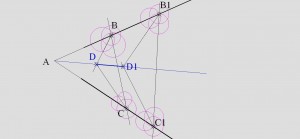
Цитата Ира (  ) 2.Через т. В проведем прямую, пересекающую стороны угла А, получим точки Д и С. Проведем через них прямые, параллельные АС и АД соответственно, получим т. Е. От С отложим отрезок CB1 равный ДВ и соединим B1 с Е. Искомая прямая ВА будет параллельна B1E.
Тут Ваше решение существенно сложнее, и вы достроили зеркальное отображение вершины угла. Если честно я не знаю засчитали бы Ваше построение, так как оно ничем не отличается от построения самой вершины.
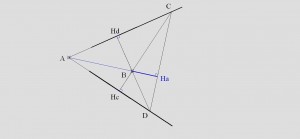
Высоты треугольника пересекаются в одной точке:
1. опускаем из точки В перпендикуляры на стороны угла.
2.Продолжаем эти перпендикуляры до пересечения с противоположными сторонами угла.
3. Соединяем полученные точки.
4. На полученный отрезок опускаем перпендикуляр из точки В. Полученный перпендикуляр будет принадлежать прямой которой принадлежит АВ.
Следует заметить, что эти задачи действительно могут присутствовать на ЕГЭ, для их решения достаточно знать что биссектрисы и высоты треугольника пересекаются в одной точке. Но, так как школьник, практически не сталкивается с задачами на построение, даже такие элементарные задачи могут вызвать затруднение.
Третья задача не решается только на школьных знаниях, подумаете или ответ дать?
Приношу извинения за то что долго не отвечал, на данном форуме задачами по геометрии явно не интересуются.
Сообщение отредактировал Race - Пт, 24.02.17, 12:26 |
| |
| |
| Ира | Дата: Пт, 03.03.17, 14:25 | Сообщение # 4 |

Гуру  Сообщений: 260
Совы: 6 
| Race, да, согласна, теперь я вижу, что перемудрила. И буду признательна, если Вы сообщите решение третьей задачи.
|
| |
| |
| Race | Дата: Пт, 03.03.17, 22:33 | Сообщение # 5 |

Просветленный  Сообщений: 459
| Цитата Ира (  ) Race, да, согласна, теперь я вижу, что перемудрила. И буду признательна, если Вы сообщите решение третьей задачи.
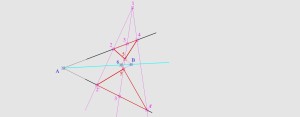
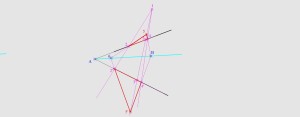
Точки пронумерованы по мере построения.
1. Выбираем произвольную точку за границами угла, пусть это будет т.1.
2. Из этой точки строим три луча, таким образом, что бы они пересекали обе стороны угла и не проходили через точку В., получаем точки 2, 2', 3, 3', 4, 4'.
3. Выбираем одну из пар точек, таким образом, что бы построенный из него луч пересекал любой другой луч, которому принадлежит любая другая пара до прохождения точки В. Строим этот луч, в нашем случае из т. 2 и 2'. Получили точки 5 и 5'.
4. Из 3ьего луча строим луч через точки 5 и 5'. Пусть точка пересечения этих лучей будет т.6.
5. Соединяем точку 6 и В, этот отрезов принадлежит отрезу АВ.
Интересно, лучи и треугольники можно строить любым образом, как за пределами угла, так и внутри его. Лучи можно строить таким образом, что бы точка В была внутри любых двух, так и снаружи.
|
| |
| |
| Ира | Дата: Пн, 06.03.17, 22:51 | Сообщение # 6 |

Гуру  Сообщений: 260
Совы: 6 
| Красотища! Спасибо. А теорема эта впервые встретилась мне.
|
| |
| |
| Race | Дата: Вт, 07.03.17, 13:26 | Сообщение # 7 |

Просветленный  Сообщений: 459
| Цитата Ира (  ) Красотища! Спасибо. А теорема эта впервые встретилась мне.
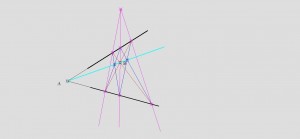
Тут на сколько я понимаю построение идет таким образом, сначала строятся красные прямые, проходящие через В, затем через точки пересечения этих прямых с сторонами угла, строятся крайние фиолетовые, из точки пересечения фиолетовых строится средняя фиолетовая проходящая через точку В. Последними строятся синие, точки пересечения синих, как и точка В принадлежат прямой которой принадлежит АВ.
|
| |
| |
| Oleg4922 | Дата: Ср, 08.03.17, 01:03 | Сообщение # 8 |

Гуру  Сообщений: 101
Совы: 2 
| Ещё одно несложное решение первой задачи. Как загрузить со смартфона на сайт картинку не знаю, поэтому попытаюсь объяснить на словах.
Необходимо каждому лучу с двух сторон на одинаковом расстоянии провести по две параллельные прямые (сделать это несложно например с помощью двух перпендикуляров каждому лучу), после чего соединить точку пересечения полученных двух внутренних в угле прямых с точкой пересечения двух наружных прямых. Так мы получим искомую биссектрису.
Вторая задача решается аналогично, хотя и несколько сложнее. Прямые параллельные лучам должны быть не на одинаковых расстояниях от лучей, а на расстояниях равных кратчайшим расстояниям от точки В до лучей. Попробуйте это несложно.
|
| |
| |
| Race | Дата: Пт, 19.05.17, 11:03 | Сообщение # 9 |

Просветленный  Сообщений: 459
| Oleg, а чем это отличается от построения самого угла? Достраивать не сложно, понадобится всего лишь линейка. Попробуйте, это еще проще.
Добавлено (12.04.2017, 20:33)
---------------------------------------------
Придумал новую задачу))) Как раз на медианы.
Дано:
Острый угол А (можно даже с недоступной вершиной)
т. N, про которую известно что она является центром пересечения медиан треугольника АВС, который был ранее построен на сторонах угла А.
Задача - построить данный треугольник.
Добавлено (14.04.2017, 08:10)
---------------------------------------------
Что, даже идей ни у кого нету?
Вся информация необходимая для построения, как и в 1 двух задачах, дается школьнику еще в 8 классе...
Добавлено (19.05.2017, 11:03)
---------------------------------------------
Продолжаем умничать.
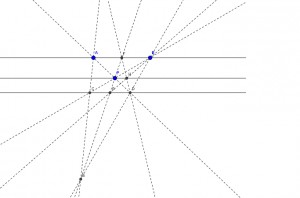
Даны две параллельные прямые a и b, и точка А не принадлежащая прямым.
При помощи одной только линейки построить прямую с, проходящую через т. А и параллельную a и b.
Сообщение отредактировал Race - Пт, 19.05.17, 11:03 |
| |
| |
| zhekas | Дата: Вт, 23.05.17, 08:12 | Сообщение # 10 |

Гуру  Сообщений: 166
Совы: 6 
| 
|
| |
| |































