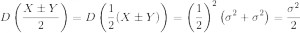Квадрат стандартного откланения показывает на сколько в среднем некоторая случайная величина отличается от среднего значения некоторого набора случайных величин.
Поэтому при вычислении объёма кирпича, после непосредственного измерения трёх его ребер, не надо ничего складывать или умножать. Точность не изменится при изменении количества измерений.
Возьмём кирпич и нашу бракованную линейку, начнём измерять длину, ширину и высоту кирпича начиная с первого деления линейки, вычислим объёме кирпича (х₁ ) (назовём это ,- эксперименэт 1), проделаем эксперимент 2, - измерим длину, ширину и высоту кирпича начиная со второго деления линейка, вычислим объём кирпича (х ₂), продолжаем эксперименты в том же духе,.
Запишим полученные объёмы:
x₁,x₂,...,x_n
далее вычисля стандартное отклонение(см.пост 5), получим ту же σ , что и в условии задачи.

Из определения стандартного отклонения интуитивно кажется, что повысить точность измерения в нашем случае нельзя, однако интуиция порой обманчива.
Известно что
1) σ²=D(X), где D(X) - дисперсия случайной величины X(x₁,x₂,...,x_n)
Так же из свойств дисперсии известно, что
2) D(aX±bY)=a²D(X)+b²D(Y)±2abcov(X,Y)
Где a и b некоторые константы.cov(X,Y) - ковариация между случайными величинами X(x₁,x₂,...,x_n) и Y(y₁,y₂,...,y_n)
Проделаем измерения следующим образом:
Измерим общую длину обоих кирпичей приставив их друг к другу. Полученный результат обозначим буквой Х.
Теперь приставим кирпичи друг к другу так, чтобы померить разность длин кирпичей, полученный результат обозначим Y.
Таким же образом замеряем ширину и высоту кирпичей.
Не трудно видеть что длину(ширину, высоту) каждого из кирпичей можно найти по следующим формулам
,
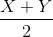
Таким образом дисперсия полученных величин
согласно (1) и (2), будет равна

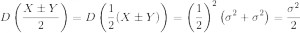
Из (1) ясно, что при таком способе измерения мы повысили точность практически на треть (σ/√2).
P.S. т.к. в нашем случае X и Y независимы, то cov(X,Y)=0
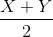