| Race | Дата: Среда, 26.10.2016, 12:01 | Сообщение # 21 |
Просветленный  Сообщений: 459
| Rostislav, а интересно, Ваше решение предусматривало теорему Декарта?
Если не секрет конечно.
Добавлено (26.10.2016, 12:01)
---------------------------------------------
Кстати. Тут коллегиальными усилиями, как одно из следствий построение искомой окружности методом инверсии, получилось еще одно решение.
Особо одаренные могли бы решить данную задачу как:
Из точки С (центр окружности а) провести окружность радиуса ra+1/2rb
Из точки М (центр окружности b) провести окружность радиуса 3/2 rb
Центр искомой окружности будет находиться на пересечении 2 построенных окружностей, а радиус равняться половине радиуса окружности b.
rc=5(1.5-sqr2)
Соответственно точная площадь окружности будет равна:
Sс=П(rc)2=25П(4,25-3sqr2)
(с) Все совпадения в манере изложения результата случайны, закономерности надуманны. Кол-во полезной информации исторически совпадает.
Сообщение отредактировал Race - Среда, 26.10.2016, 12:24 |
| |
| |
| Race | Дата: Вторник, 09.01.2018, 16:10 | Сообщение # 22 |
Просветленный Сообщений: 459
| Так, я тут полгода назад подкинул данную задачку на другой форум) Решение оказалось достаточно тривиальным) сам удивляюсь как его умудрился зевнуть.
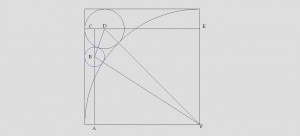
Пусть радиус четверти окружности - R
Радиус средней окружности - r
Радиус меньшей окружности - x
Отрезок CB - l
По т-ме Пифагора (мде... для решения задачи использовал т-му Декарта, инверсию, степени точек, позорище)
Для треугольников:
ABF: (R+x)2=(R-x)2+(R-r-l)2 => (R-r-l)2=4Rx => R-r-l=2sqrt(Rx) (1)
DEF: (R+r)2=(R-r)2+(R-r)2 => R+r=sqrt2(R-r) => r=R(sqrt2-1)/(sqrt2+1) (2)
CDB: (r+x)2=(r-x)2+l2 => l2=4rx => l=2sqrt(rx) (3)
Подставим (3) в (1)
R-r-2sqrt(rx)=2sqrt(Rx) => sqrtx=(R-r)/[2(sqrtR+sqrtr)] => x=(R-r)2/[4(sqrtR+sqrtr)2] (4)
Подставив (2) в (4) получаем значение радиуса синей окружности)
Сообщение отредактировал Race - Вторник, 09.01.2018, 16:32 |
| |
| |
