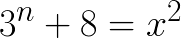FAQ по форумуНовые сообщения на Форуме
  • Страница 1 из 3
  • 1
  • 2
  • 3
  • »
Форум Эрудитов » Логические задачи и головоломки » Математические задачи » Решенные задачи » Уравнение (sml[ok])
Уравнение
erudite-manДата: Пт, 06.05.16, 14:15 | Сообщение # 1
Модератор
Сообщений: 1378
Награды: 244
Найдите все целые корни уравнения:
Прикрепления: 8648189.png (1.0 Kb)


Сообщение отредактировал erudite-man - Вс, 08.05.16, 12:35
 
никникДата: Пт, 06.05.16, 16:17 | Сообщение # 2
Высший разум
Сообщений: 2770
Награды: 406
Совы: 15
n=0, x=3
Что очевидно:
если есть еще х, то это не четное число,(а n Четное(?)
не кратное 3, (кратное 11 или 17(?)
Между своеобразной логикой и откровенной глупостью иногда очень тонкая грань.
 
erudite-manДата: Пт, 06.05.16, 16:21 | Сообщение # 3
Модератор
Сообщений: 1378
Награды: 244
Корни вы нашли, теперь неплохо бы грамотно и логично доказать, что при n ≠ 0 корней нет.
 
никникДата: Пт, 06.05.16, 22:26 | Сообщение # 4
Высший разум
Сообщений: 2770
Награды: 406
Совы: 15
(3n/2-x)(3n/2+x)=-8
при четном n
(3n/2+x)и|3n/2-x| целые сомножители 8: 2 и 4 либо 1 и 8,т.е. n<4
Между своеобразной логикой и откровенной глупостью иногда очень тонкая грань.

Сообщение отредактировал никник - Пт, 06.05.16, 22:45
 
erudite-manДата: Сб, 07.05.16, 09:51 | Сообщение # 5
Модератор
Сообщений: 1378
Награды: 244
Цитата никник ()
(3n/2-x)(3n/2+x)=-8при четном n
(3n/2+x)и|3n/2-x| целые сомножители 8: 2 и 4 либо 1 и 8,т.е. n<4
не понимаю wall
кстати, я только сейчас заметил, Вы ещё один корень потеряли:
x2 = 9
x1 = 3, x2 = -3
 
ArtchiДата: Сб, 07.05.16, 10:15 | Сообщение # 6
Гуру
Сообщений: 202
Награды: 5
Совы: 0
А программно подойдёт? 
X проверяется:  X div 2 = 1 (нечёт), =0 (четное число)
И ставим цикл для N (while.. do)
Ломая стереотипы....
 
erudite-manДата: Сб, 07.05.16, 10:24 | Сообщение # 7
Модератор
Сообщений: 1378
Награды: 244
Если вы сможете с помощью цикла while проверить все n ∈ ( -∞; +∞), то пожалуйста.
Но вообще, это уравнение - 19-е задание ЕГЭ по математике, желательно решить его математически.
 
ArtchiДата: Сб, 07.05.16, 10:41 | Сообщение # 8
Гуру
Сообщений: 202
Награды: 5
Совы: 0
Смогу, а почему нет-то? Эрудитмен
Ломая стереотипы....
 
erudite-manДата: Сб, 07.05.16, 10:47 | Сообщение # 9
Модератор
Сообщений: 1378
Награды: 244
жду с нетерпением Ваш код
 
ArtchiДата: Сб, 07.05.16, 11:08 | Сообщение # 10
Гуру
Сообщений: 202
Награды: 5
Совы: 0
n: null;
x: extended; 
бла бла бла

While (N not div 2<> 1) do
X<> целому числу. 
И так до конца, причем здесь бесконечность.
Если в цикле можно поставить хоть 1<>1 i:=i+1 Break только его "угомонит"
Ну или free
Ломая стереотипы....
 
Форум Эрудитов » Логические задачи и головоломки » Математические задачи » Решенные задачи » Уравнение (sml[ok])
  • Страница 1 из 3
  • 1
  • 2
  • 3
  • »
Поиск:

Интересная информация
Последние задачи Сообщество эрудитов ВКонтакте Рейтинг сообщений Совиный рейтинг
1.Твоя теория48
2.Арнольд, да не тот80
3.Брэндон.3
4.Задача с матрицами3
5.Простенький вопросик10
6.Гидродинамика15
7.Быстрая река.24
8.А попробуйте ещё это опро...6
9.Задача по логике7
10.Головоломка без ключа2
1.Rostislav5379
2.Lexx4728
3.nebo3639
4.Иван3061
5.никник2770
6.Kreativshik2472
7.Гретхен1807
8.Vita1583
9.erudite-man1378
10.Valet937
1.nebo123
2.Kreativshik113
3.sovetnik49
4.MrCredo38
5.IQFun30
6.Pro100_Artyom27
7.marutand20
8.хан20
9.никник15
10.Фигаро15

ГлавнаяГостевая книгаFAQОбратная связьКоллегиФорум Эрудитов