|
Вызов сайту Эрудитов от Алексея
|
|
| zhekas | Дата: Чт, 17.11.11, 00:39 | Сообщение # 11 |

Гуру  Сообщений: 166
Совы: 6 
| Можно и по другому
пусть P(n) -> p при n -> бесконечтности
Возмём какое-нибудь n и найдём вероятность что мы не попадём на это число. То есть перескочим через него.
Мы обязательно попадём в один из 6-и номеров
n-6) Вероятность перескочить из него через n равна нулю. Больше 6-и мы никак не выбьем.
n-5) 1/6
n-4) 2/6
n-3) 3/6
n-2) 4/6
n-1) 5/6
То есть вероятность перескочить через n равна
P(n-6)*0+P(n-5)*1/6+P(n-4)*2/6 + P(n-3)*3/6 + P(n-2)*4/6 + P(n-1)*5/6
С другой стороны, вероятность перескочить через n равна 1-P(n)
Получили равенство
P(n-6)*0+P(n-5)*1/6+P(n-4)*2/6 + P(n-3)*3/6 + P(n-2)*4/6 + P(n-1)*5/6 = 1 - P(n)
устремляем n к бесконечноти, тогда все P(n-k) устремятся к p и у нас получится равенство
p*0+p*1/6+p*2/6 + p*3/6 + p*4/6 + p*5/6 = 1- p
p*15/6 = 1 - p
p*21/6 = 1
p=6/21 = 2/7
|
| |
| |
|
| zhekas | Дата: Вс, 20.11.11, 06:16 | Сообщение # 13 |

Гуру  Сообщений: 166
Совы: 6 
| 3) У нас есть пара одинаковых тетраэдров
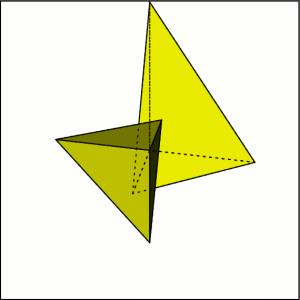
Точки первого тетраэдра задаются с помощью трёх направляющих векторов a,b,c
M1=t1*a+p1*b+q1*c
где
0<=t1<=1
0<=p1<=1-t1
0<=q1<=1-t1-p1
Второй тетраэдр также задаётся с помощью этих же векторов
M2=t2*a+p2*b+q2*c
но
-1<=t1<=0
-1-t1<=p1<=0
-1-t1-p1<=q1<=0
тогда середина отрезка M1M2 опять же задаётся через эти векторы
M=((t1+t2)/2)a+((p1+p2)/2)b+((q1+q2)/2)c
или если сделать соответствующие замены
M=t*a+p*b+q*c
В соответствующих октантах t,p,q будут менятся следующим образом
1)t,p,q>=0
0<=t<=1/2
0<=p<=1/2-t это тетраэдр со сторонами в два раза меньше исходных
0<=q<=1/2-t-p его объём равен 1/8 объёма исходного тетраэдра
2)t,p,q<=0
-1/2<=t<=0
-1/2-t<=p<=0 тоже что и в слечае 1
-1/2-t-p<=q<=0
3) t,p>=0 q<=0
0<=t<=1/2
0<=p<=1/2-t это призма с основанием треголиником, основаннном на векторах 1/2a 1/2b
-1/2<=q<=0 и боковому ребру равному 1/2c Её объём составляет 1/8 исходного тетраэдра
4,5,6,7,8) получаются призмы с обёмом 1/8 исходного тетраэдра
итого объём получившейся фигура:
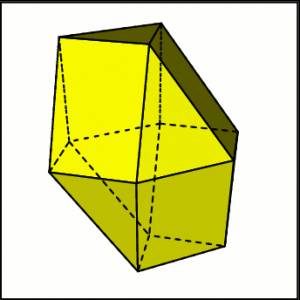
равен 2*(1/8) + 6*(3/8) = 5/2 объёма исходного тетраэдра
5/2*2010=5025
Сообщение отредактировал zhekas - Вс, 20.11.11, 06:18 |
| |
| |
|
|




























