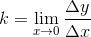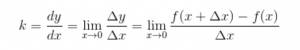Найти косательную к окружности довольно просто, она всегда перпендикулярна радиусу, а как аналитически найти касательную к кривой?
Из геометрии известно, что любую кривую можно задать аналитически некоторой функцией y=f(x). Например прямая задается выражением y=kx+b, где k-угловой коэффициент, b-отрезок отсекаемый прямой на оси ординат.
Очевидно, что изменение x на какую-то величину Δx, приводит к изменению y на величину Δy, поэтому можно записать
(1)y+Δy=f(x+Δx), тогда
(2) Δy=f(x+Δx)-y
или
(3)Δy=f(x+Δx)-f(x)
Эти три выражения надо запомнить.
На рисунке это можно изобразить так

Таким образом касательная к кривой в точке с координатами [x;f(x0)](обзавем ее А) это предельный случай секущей, при вращении которой вокруг точки А , точка пересечения секущей с кривой полностью совподает с А. Угловой коэффициент здесь соответствует tg(α), т.е из определения тангенса, угловой коэффициент равен отношению
k=Δy/Δx
Таким образом угловой коэффициент касательной равен
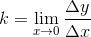
Лейбниц предложил записать это выражение как
k=dy/dx
dy и dx обязывают дифференциалами. Разницу между dy и Δy можно увидеть на следующем рисунке
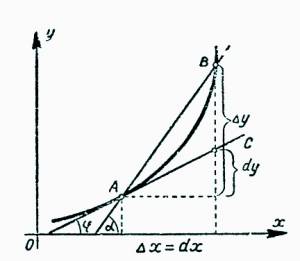
Таким образом можно записать
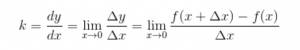
Этот самый угловой коэффициент и есть производная.
Найти производную какой-либо функции не столь трудно(в принципе есть таблицы производнах)
В данной задаче нам была дана парабола, которой как известно отвечает уравнение y=x²
Найдём производную данной функции, для этого вспомним те три выражения
(1),(2),(3) записанные в начале данного поста.
Теперь пойдём поэтапно
1) найдём приращение Δx:
y+Δy=(x+Δx)²=x²+2xΔx+Δx²
2) найдём приращение Δy:
Δy=2xΔx+Δx²
3) Найдём Δy/Δx:
(2xΔx+Δx²)/Δx=2x+Δx
4) устремляем Δх к 0(Δх→0), то есть найдём dy/dx:

Таким образом 2х есть производная функции y=x², т.е. 2х это тангенс угла между положительным направлением оси х и касательной к параболе в точке с координатами [х;у=х²]. В общем случае производная функции y=xⁿ равна nх
n-1