|
Велодорожка
|
|
| Race | Дата: Вс, 06.11.16, 11:53 | Сообщение # 141 |

Просветленный  Сообщений: 459
| Цитата никник (  ) Race, ужасно не люблю говорить за других, но я вижу такую закономерность: когда Ваш пост в той или иной мере можно расценить, как нападки или претензии к одному из участников форума, nebo, считает своим долгом ответить за отсутствующего
Так же я не ожидал, что вопрос к участнику темы по поводу способа решения, либо построения является чем то неудобным, либо противозаконным.
Впредь постараюсь не задавать подобные вопросы.Цитата никник (  ) Если бы мне это не было затруднительно, я бы их сразу нарисовал. Их 2, один получится если соединить дальние края рисунка, так чтобы совпали дальние края квадратов, другой если совместить два треугольника лежащие по разные стороны внутренней границы между квадратами. Ну и, возможно, потом есть смысл составить 3, чтобы найти длину оставшехся перемычек. Но, там скорее всего, откроется путь проще.
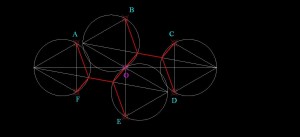
Построил все параллелограммы, которые смог представить, в синих мы знаем углы между основаниями и 1 диагональ, в параллелограммах построенных на зеленых отрезках мы знаем только углы.
Я все равно не понимаю каким образом вы предлагаете мне произвести вычисление отрезков необходимых для определения длины пути.Добавлено (06.11.2016, 11:53)
---------------------------------------------
P.S. Есть более быстрое решение, выложил его в конце 139го поста. Алгебраическое решение получается буквально в 3 этапа.
Правда предварительно задачу необходимо решить геометрическим образом.
|
| |
| |
| Race | Дата: Вс, 06.11.16, 21:33 | Сообщение # 142 |

Просветленный  Сообщений: 459
| Цитата никник (  ) И какая же разница в топологии рис. из поста 105 и Вашего чертежа, чтобы говорить о неточности геом. модели?А результат, к слову, будет иным только если неправильна сама модель, иногда и неверными способами получают верные результаты.
Я попытался найти еще одно соотношение треугольников расположенных на центре прямоугольника, при каких мы получим одну прямую, а не 2, но не смог. С другой стороны, при ином соотношении,отличном от 1 к 1, общую длину дорожки возможно получить меньше чем у nebo. В этом случае только один угол в сети получается отличным от 120, причем в большую сторону, что не противоречит условиям построения дерева Штейнера.
1 к 4 S=4,6389
3 к 7 S=4,6313
1 к 2 S=4,6294
2 к 3 S=4,6267
Видим, что по мере приближения к 2 одинаковым треугольникам общая длина уменьшается.
Сообщение отредактировал Race - Вс, 06.11.16, 21:34 |
| |
| |
| Race | Дата: Пн, 07.11.16, 10:34 | Сообщение # 143 |

Просветленный  Сообщений: 459
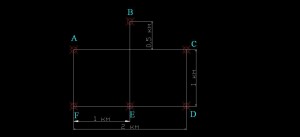
| При помощи теоремы Торричелли и Кавальери возможно доказать, что для прямоугольника и 6 точек на нем расположенных, дерево Штейнера, в котором все углы будут равны 1200 будет лишь одно, если располагать его согласно предложенной геометрической модели..
При решении задачи построения минимальной сети между расположенными в пространстве точками Торричелли и Кавальери разработали специальный механизм для построения прямых которые пересекаются под углом равным 1200.
Для 3 улицы этот механизм выглядит следующим образом:
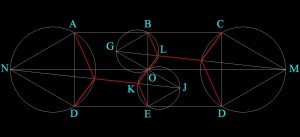
Для решения я достроил дополнительную точку, которая находится в центре пересечений диагоналей и средних линий прямоугольника. Получил равновесную систему, где все прямые пересекаются именно под углом 1200.
Причем, согласно вышеупомянутому механизму, точкой N можно заменить точки A и D, без изменения длины сети, а J точки O и E. Из чего и следует, что длина сети равна 2*NJ
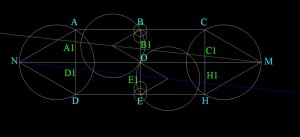
Предположим, что для нашего прямоугольника возможно построить еще одну систему подобным образом.
1. Для этого из точки N проведем произвольную секущую n которая пересечет наш прямоугольник произвольным образом, для того что бы между секущей и точкой E можно было построить отрезок под углом 1200 находящийся внутри прямоугольника, секущая должная пересечь BE.
2. Из точки М проведем секущую m, параллельную n.
3. Так как все углы между прямыми составляющими сеть равны 1200, то на n и m должны находиться 2 из прямых составляющих сеть.
4. В силу параллельности n и m, углы между ними и NM одинаковы.
5. Трапеции полученные пересечением секущих нашего прямоугольника, подобны и равны между собой.
6. ВВ1=ЕЕ1.
7. Построим из точки Е или В секущую, под углом 600 к ВЕ, до пересечения с n или m, мы получим 2 точку равностороннего треугольника из механизма Торричелли и Кавальери, после чего на полученной стороне строим равносторонний треугольник.
8. Равносторонние треугольники построенные на секущих n и m одинаковы между собой.
9. В случае если секущие n и m не параллельны между собой можно построить множество вариантов сети, только не все отрезки в ней будут соединяться под углом равным 1200.
10. Для сети которая проходит через центр пересечения диагоналей прямоугольника, можно построить только одну сеть, где все прямые пересекаются под углом 1200.
Сообщение отредактировал Race - Пн, 07.11.16, 10:45 |
| |
| |
| Vita | Дата: Пн, 07.11.16, 11:08 | Сообщение # 144 |
Гений  Сообщений: 1587
| Race, красиво и надеюсь правильно! Можно немножко сэкономить на новогодних гирляндах 
Сообщение отредактировал Vita - Пн, 07.11.16, 11:28 |
| |
| |
|
| Vita | Дата: Пн, 07.11.16, 16:13 | Сообщение # 146 |

Гений  Сообщений: 1587
| 
|
| |
| |
| Race | Дата: Пн, 07.11.16, 17:36 | Сообщение # 147 |

Просветленный  Сообщений: 459
| Vita! Вы нашли еще одно подтверждение теории озвученной Креативщиком, в мире оказывается, все прямые сходятся под углом 1200.... Вот как так, живешь, живешь и не замечаешь этого, а потом как будто глаза открываются.
Жаль сопрамат и строймех уже забыл, было бы интересно просчитать что выгоднее блок с диагональными перекрытиями, либо было с перекрытием в виде минимальной сетки.
Кстати, оба решения поставленной задачи, которые я пока получил, так же похожи на соты)
Сообщение отредактировал Race - Пн, 07.11.16, 17:37 |
| |
| |
| Race | Дата: Пн, 07.11.16, 18:13 | Сообщение # 148 |

Просветленный  Сообщений: 459
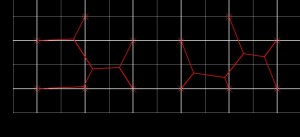
| Для моей задачи пока получилось 2 ответа.
1. S=5.1651(км.)
2. S=5.0867 (км.)
Не оставим жителей 4ой улицы без дорожек, поможем миром.
|
| |
| |
| Race | Дата: Вт, 08.11.16, 09:51 | Сообщение # 149 |

Просветленный  Сообщений: 459
| Используя симметрию точек, можно строить дерево Штейнера, даже для большего числа точек) Там где без симметрии надо было бы строить множество деревьев, для симметрично расположенных точек, на мой взгляд, достаточно построить минимальное дерево для симметричного участка. Может не прав конечно, но красиво выходит.
S=9,7848 (км.)
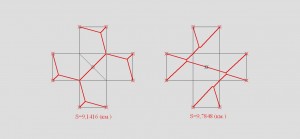
Нашел более оптимальную сеть)))
S=9,1416 (км.)
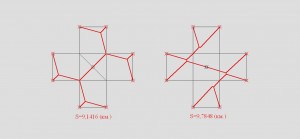
Действительно чем больше точек тем больше разнообразие и поиск оптимальной цепи можеь быть бесконечным.
Не сложно заметить, что этот вариант является объединением варианта минимального дерева Штейнера для 3 точек.
Как подозреваю он далеко не минимальный.
Сообщение отредактировал Race - Вт, 08.11.16, 10:42 |
| |
| |
| Race | Дата: Вт, 08.11.16, 10:55 | Сообщение # 150 |

Просветленный  Сообщений: 459
| И последняя, прямо кабалистический знак, но явно не оптимальная.
S=10,1962(км.)
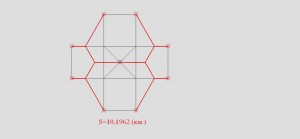
Еще одна не оптимальная сеть.
Вроде построил все или почти все симметричные сети, остались не симметричные.
S=9,4924(км.)
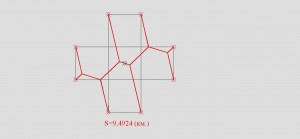
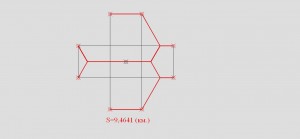
А этот прямо имперский штурмовик, получил разбиением точек на 2 группы из 3 и 5 точек.
S=9,4641(км.)
Не смотря на то, что такое решение не удовлетворяет условиям данной задачи, тем не менее это все равно дерево Штейнера
Сообщение отредактировал Race - Вт, 08.11.16, 11:18 |
| |
| |