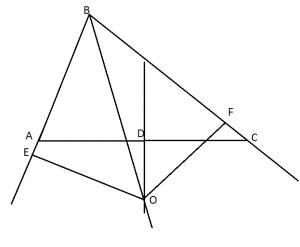
тогда точка Е может лежать на продолжении, и из твоего "доказательства" это и получается: Возьмём обычный треугольник, не равносторонний где АВ<BC.
Проведём через сторону AC серединный перпендикуляр. Он пересечёт сторону в точке D.
Проведём из вершины В биссектрису. Она пересечёт серединный перпендикуляр в точке О.(как я раньше доказала она вне треугольника)
Соединим вершины А и О; С и О.
Проведём из точки О высоты к сторонам АВ и ВС.
Рассмотрим треугольники ЕВО и FBO. Они прямоугольные, у них общая сторона ОВ и углы возле вершины В равны. Следовательно, они равны по трём углам и стороне. ЕВ=BF.
Рассмотрим треугольники AOD и COD. Они прямоугольные, у них общая сторона OD, AD=DC по построению. Значит, они равны как прямоугольные треугольники по двум катетам.
Рассмотрим треугольники ЕОА и FOC. Они прямоугольные, у них АО=СО и EO=FO. Значит, они равны как прямоугольные треугольники по двум катетам. АЕ=СF.
"BE+EA=ВF+FC => треугольник ABC равнобедренный."-ЭТО НЕВЕРНО!!!
AB<BC, BE+EA=ВF+FC => точке Е лежит на продолжении АВ, а точка F на отрезке ВС
Всё доказанное было верно но вывод из этого был сделан неправильный
От этого разве меняется доказательство? Треугольник равнобедренный, всё совпадает, окей. Всё равно же мы доказали, что любой треугольник равнобедренный. Тут очень прикольный ответ. В доказательстве встречается вещь по типу "ну, дальше здесь получается 2х2=5, это и так всем понятно, мы идём в треугольник, тут применяем теорему...". 
