|
Сумма углов под которыми виден отрезок в треугольнике
|
|
| Race | Дата: Вс, 01.04.18, 14:12 | Сообщение # 1 |

Просветленный  Сообщений: 459
| На плоскости задан равнобедренный треугольник АВС. С основанием ВС и углом α при вершине А.
Основание разбито на n+1 равных отрезков n точками Pi (i принимает значение от 1 до n и Є N).
Чему равна сума углов под которыми из точек Pi виден отрезок AP расположенный на стороне АВ если |AP|=|AB|/(n+1).
Задача честно скомунизжена с другого форума, где публиковалась как несколько усложненная задача с школьной олимпиады. Впоследствии была еще немного усложнена мной. Приятного решения.Добавлено (01.04.2018, 14:12)
---------------------------------------------
Давайте упростим до уровня школьной олимпиады.
Треугольник правильный. n=4.
|
| |
| |
| nebo | Дата: Ср, 04.04.18, 15:25 | Сообщение # 2 |

Высший разум  Сообщений: 3639
| Цитата Race (  ) Треугольник правильный. n=4.
12гр.+9гр.+6гр.+3гр.=30гр.
|
| |
| |
| Race | Дата: Ср, 04.04.18, 15:41 | Сообщение # 3 |

Просветленный  Сообщений: 459
| Ответ верный, но как Вы определили углы?
Правда если мне не изменяет память углы там выходят отнюдь не целые ;—)
|
| |
| |
| nebo | Дата: Ср, 04.04.18, 19:13 | Сообщение # 4 |

Высший разум  Сообщений: 3639
| Я с чего-то решила, что углы, образованные при делении вершин треугольников будут равны, соответственно 12 и 15 градусов.
Ваше замечание поставило меня в тупик. Потом разобравшись, стало ясно, что они равны попарно, начиная с обоих сторон.
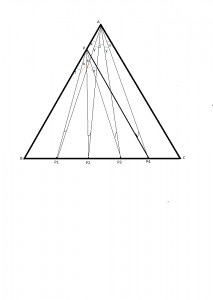
Итак, смотрим картинку,
картинка слегка запоздала и оказалась в следующем посте)))))
ΔBPP4 подобен заданному, конечно, можно, используя теорему косинусов, определить, что он равносторонний.
А значит ∠APP4=120 гр. (В дальнейшем я не буду писать градусы.)
Находим неизвестные углы, из которых видна AP. Совершенно необязательно знать их значения.
∠AP4P=х, здесь видно, что PP4 и AC параллельны, а AP4 диагональ.
∠AP3P=180-[(120+f)+x+y+z]
∠AP2P=180-[(120+k+f)+x+y]
∠AP1P=180-[(120+2k+f)+x
Их сумма = 180-3f-3k-2x-2y-z, что значит 180-90-60 градусов. В результате - 30 градусов.
Сообщение отредактировал nebo - Ср, 04.04.18, 19:18 |
| |
| |
| nebo | Дата: Ср, 04.04.18, 19:16 | Сообщение # 5 |

Высший разум  Сообщений: 3639
| 
Сообщение отредактировал nebo - Ср, 04.04.18, 19:18 |
| |
| |
| Race | Дата: Ср, 04.04.18, 20:26 | Сообщение # 6 |

Просветленный  Сообщений: 459
| Вот теперь абсолютно правильно! Доберусь до компьютера выдам приз.
яиндукцией легко докажите и для основной задачи
|
| |
| |
|
| nebo | Дата: Ср, 04.04.18, 20:44 | Сообщение # 8 |

Высший разум  Сообщений: 3639
| Треугольник правильный. n=4.
|
| |
| |
| Vita | Дата: Ср, 04.04.18, 20:45 | Сообщение # 9 |
Гений  Сообщений: 1585
| nebo, спасибо. Теперь понятно 
|
| |
| |
| Race | Дата: Ср, 04.04.18, 21:12 | Сообщение # 10 |

Просветленный  Сообщений: 459
| Vita,
это было решение упрощенной задачи, где треугольник равносторонний, значит углы при вершине 60 градусов, а угол P1PA равен 120 градусов.
nebo,
одно замечание - подобие треугольников ABC и P1PB доказывается через теорему Фалеса) так гораздо проще чем через теорему косинусов.
|
| |
| |
























