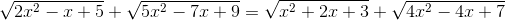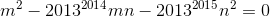K(2x^2-x+5)-K(x^2+2x+3 = K(5x^2-7x+9)- K(4x^2-4x+7)
Возводим обе части в квадрат
K(2x^2-x+5)-K(x^2+2x+3)=(2x^2-x+5)-(x^2+2x+3)-2K(2x^4+4x^3+6x^2-x^3-2x^2-3x+5x^2+10x+15)=x^2-3x +2 - 2K(2x^4+3x^3+9x^2+7x+15)
K(5x^2-7x+9)- K(4x^2-4x+7)=x^2-3x+2-2K(20x^4-20x^3+35x^2-28x^3+28x^2-49x+36x^2-36x+63)=x^2-3x+2- 2K(20x^4-48x^3+99x^2-85x+63)
2x^4+3x^3+9x^2+7x+15=20x^4-48x^3+99x^2-85x+63
18x^4-51x^3+90x^2-92x+48=0
72x^3-153x^2+180x-92=0
18x^4+90x^2+48=51x^3+92x
18x^4+46x^2+44x^2+48=51x^3+92x
18x^4+46x^2-51x^3
x^2(18x^2-51x+46)+(44x^2-92x+48)=0
x^2(18x^2-51x+37)+(53x^2-92x+48)=0
(18x^2-51x+37)>0
(53x^2-92x+48)>0
Очень кажется,что решения нет, но надо проверять,в т.ч. не потерялись ли решения при возведение в квадрат. Вроде не должны были, т.к. подкоренные выражения больше нуля.