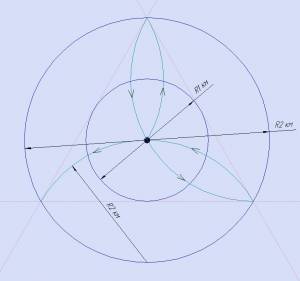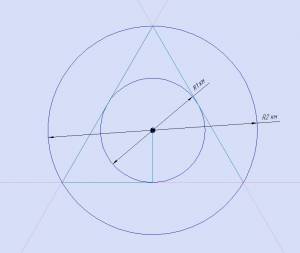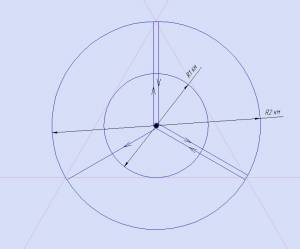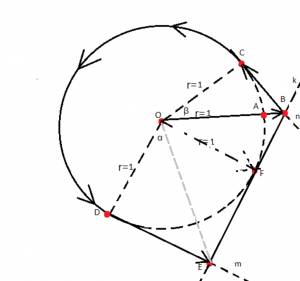
Очевидно, что если с начальной точки O пройти 1км. до точки F затем пройти по окружности с центром O и радиусом 1км. до возвращения вновь в точку F, т.е пройдём путь равным 1+2π, то по пути обязательно попадём на дорогу.
Искомая нами дорога фактически одна из касательных нашей окружности. Предполагая, что она проходит через точку F, проведём в этой точке касательную k. Возьмём на нижней части касательной k точку E таким образом, что отрезок DE, проведённой через эту точку касательной m, был бы меньше DF (естественно он будет меньше и дуги
DF- здесь и далее для обозначения дуги будем использовать подчёркивание). Аналогично возьмём на верхней части касательной k точку B таким образом, что сумма отрезка BC проведённой через эту точку касательный n и отрезка AB (AB+BC) был бы меньше FC (естественно он будет меньше и
FC). Т.к. все касательные
DF (Возможные дороги) пересекаются с DE, а все касательные
FC с BC то очевидно что, пройдя путь OABCDE, мы точно выйдем из степи. В результате получается что:
OB+BC+
CD+DE<1+2π
Фактически дальнейшая наша задача сводится к нахождению min(OB+BC+
CD+DE).
Для этого необходимо решив геометрическую задачу с применением тригонометрии привести выражение (OB+BC+
CD+DE) к виду F(α), где α в радианах. Далее найти производное первой степени F(α) – F`(α) и решив полученное тригонометрическое уравнение F`(α)=0; найти значение α, а значит и значения дуг
FC,
CD,
DF (определение точек C,B,F,E,D) а следовательно и min(OB+BC+
CD+DE).
Продожем…
Сделаем это в 2 этапа: сначала минимизируем путь – OFCDE, а затем уже OABCDE.
1.Минимизация OFCDE
Из треугольника ODE:
DE=ODtg(α)=tg(α);
Имеем также:
OF=1;
FD=2π-2α;
И так на остаётся найти α при которой:
OF+
FD+DE=1+2π-2α+ tg(α)→min
(1+2π-2α+ tg(α))`= -2+1/cos2(α)=0
1-2 cos2(α)=0
Отсюда:
α=π/4
<DOF=<DEF=2α=π/2;
Отсюда следует что:
DE=OF=1;
FD=2π-2α=3π/2
DE=tg(π/4)=1;
Min(OFCDE)=2+3π/2=6,71
А теперь приступим к минимизации OABCDE т.е. OB+BC+
CD+DE
DE=1;
CD=
FD-
FC=3π/2-2β;
Из треугольника OBC имеем:
OB=sec(β);
BC=tg(β):
OB+BC+
CD+DE= sec(β)+ tg(β)+ 3π/2-2β+1 →min;
(sec(β)+ tg(β)+ 3π/2-2β+1)`=1/cos2(β)+tg(β)/cos(β)-2=1+cos(β)tg(β)-2cos2(β)=0
Отсюда:
β=π/6;
<COF=2β=π/3;
OB=sec(π/6)=2√3/3;
BC=tg(π/6)=√3/3;
CD=3π/2-π/3=7π/6;
DE=1;
min(OABCDE)=min(OB+BC+
CD+DE)= 2√3/3+√3/3+7π/6+1=6,39
ответ: 6,39км.