Для тех кто забыл, напомню, вот это числовая ось действительных чисел:
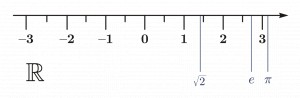
Мир куда более богаче обычной одномерной прямой, поэтому зацикливаться на ней, в то время когда есть возможность как минимум посмотреть по сторонам это просто преступление против здравого смысла. Оглядимся и увидим что по сторонам от этой оси тоже есть числа:
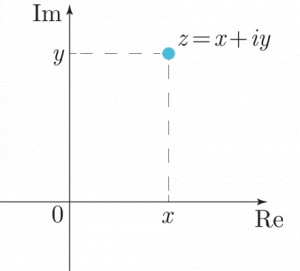
которые можно представлять как координаты (x, y) на плоскости.
Но мы для удобства перейдём в полярные координаты, и тогда новые необычные числа мы будем представлять радиус вектором (модуль комплексного числа) и естественно углом φ (аргумент комплексного числа) на который модуль отстоит от известной нам числовой оси (против часовой стрелке). Выделим на нашей плоскости единичную окружность, к которой мы привыкли, тогда можно (не вдаваясь в подробности) определить через знакомые всем синус и косинус, знаменитое тождество Эйлера
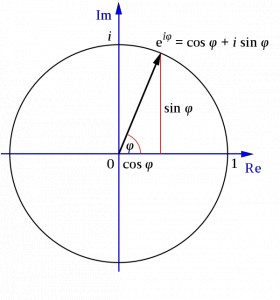
Можно видеть, что если φ=π, то sin(π) =0, а cos(π) =-1, Таким образом e
iπ=-1, а например e
i2π=1, ну и естественно e
i2πn=1
исходя из этого перепишем наше уравнение следующим образом
e
i2πnx=2
прологарифмируем данное выражение
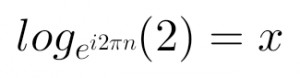
Заменим основание логарифма (формулу все помнят надеюсь)
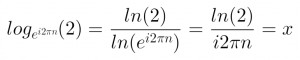
по идее нужно избавится от иррациональности, переносом i в числитель
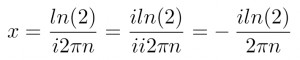
но это в данном случае не обязательно
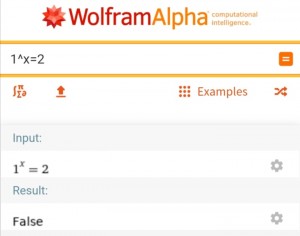
Ну а теперь можно уже задать правильный вопрос вольфоаму
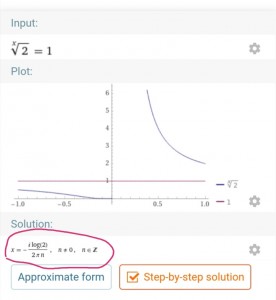
и как видим получили правильный ответ.
Понятно, что количество решений равно количеству n, т. е. их бесконечно много и ещё чуть-чуть. Понятное дело что среди решений есть и решение при котором получается 2.
Чтобы не углубляться в детали и не писать здесь кучу непонятных слов, я просто запишу этот результат (n=1)
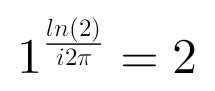
.
Проверяем на вольфраме
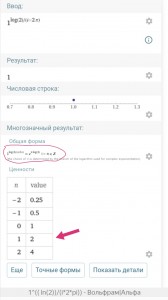
как видим при правильно поставленном вопросе вольфрам даёт всё что знает об ответе.
Всем спасибо за участие.















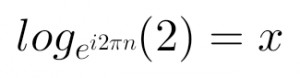
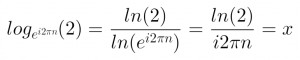
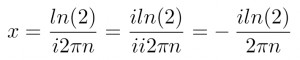

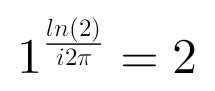 .
.






