|
Почертим? (без циркуля)
|
|
| Race | Дата: Пт, 15.09.17, 10:59 | Сообщение # 1 |

Просветленный  Сообщений: 459
| К моей большой жалости новые, интересные, задачи на данном ресурсе появляются все реже и реже.
К сожалению, в данный момент, я только повторяю школьную алгебру, потому могу выкладывать задачи лишь по геометрии, а их никто не хочет решать.
Тем не менее предприму еще одну попытку.
Всем известно, что при черчении используется два основных инструмента: циркуль и линейка, а давайте представим, что циркуля у нас нету и попробуем почертить используя одну безразмерную притом бесконечную линейку.
На данный момент времени накопился целый раздел задачек на эту тему. Если найду тут тех кто заинтересуется буду выкладывать.
Начну с самого простого, так сказать, с основ.
1. Дан отрезок и параллельная ему прямая.
а) определить центр отрезка (поделить его на 2 части).
б) удвоить отрезок.
2. Даны две параллельных прямых и произвольная, не принадлежащая прямым точка.
построить через точку прямую параллельную заданным.
|
| |
| |
| erudite-man | Дата: Пт, 15.09.17, 11:50 | Сообщение # 2 |

Модератор
Сообщений: 1378
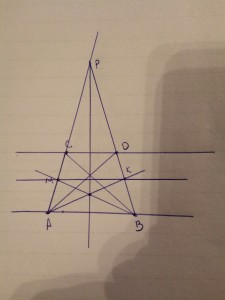
| 1. а) 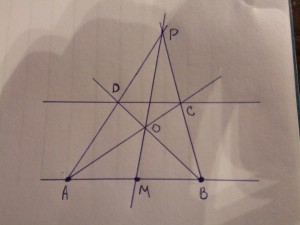
Разделяемый отрезок - AB.
Строим на прямой произвольные точки C и D и проводим через них прямые AD и BC. Получаем трапецию ABCD.
Продолжаем боковые стороны трапеции до пересечения в точке P.
Проводим диагонали трапеции, точка пересечения - O.
Зная, что середины оснований и точки пересечения диагоналей и боковых сторон лежат на одной прямой, проводим прямую OP. Она пересекает AB в точке M.
Таким образом, точка M - середина отрезка AB.
Сообщение отредактировал erudite-man - Пт, 15.09.17, 12:46 |
| |
| |
|
|
|
| erudite-man | Дата: Пт, 15.09.17, 13:43 | Сообщение # 6 |

Модератор
Сообщений: 1378
| Цитата Race (  ) Если Вам интересно, командуйте, буду еще задачки выкладывать) 
Сообщение отредактировал erudite-man - Пт, 15.09.17, 13:53 |
| |
| |
| Race | Дата: Ср, 20.09.17, 14:47 | Сообщение # 7 |

Просветленный  Сообщений: 459
| erudit-men,
Вы абсолютно правы.
Следует заметить, что решить задачу №2 можно и другим способом, хотя предложенный Вами наиболее прост.
Немного усложняем. А то вы все по трапеции решили)
3. Даны две пересекающихся (в точке А) прямых и произвольная точка В, не принадлежащая прямым.
Построить отрезок принадлежащий прямой соединяющей А и В, при условии, что точка пересечения заданных прямых недоступна.
4. Даны 3 пересекающихся в 1 точке прямых a, b, c, известно что а перпендикулярна к с.
Удвоить угол между а и b (a^b).
Добавлено (16.09.2017, 09:20)
---------------------------------------------
Эх.... Если нужны подсказки, то пишите.
Добавлено (20.09.2017, 14:47)
---------------------------------------------
Эх, пропал запал.
Ладно, даю подсказку по 3ьей:
Любой способ при помощи которого возможно построить прямую параллельную двум другим параллельным прямым, подходит для построения прямой принадлежащей тому же пучку прямых (обзовем прямые имеющие общую точку пересечения - пучком) что и 2 произвольных прямых, можно применять и в обратном направлении, любой способ позволяющий построить прямую принадлежащую пучку, позволяет построить прямую параллельную 2 параллельным прямым.
Это обусловлено тем, что параллельные прямые можно рассматривать как пересекающиеся, но точка их пересечения бесконечно удалена. При таком допущении, все иные законы Эвклидовой геометрии продолжают выполняться.
Берете и применяете Ваш способ трапеции для параллельных, решаете задачу №3.
Самих решений, при применении одной линейки достаточно много....
Сообщение отредактировал Race - Ср, 20.09.17, 14:51 |
| |
| |
| erudite-man | Дата: Ср, 20.09.17, 21:48 | Сообщение # 8 |

Модератор
Сообщений: 1378
| Цитата Race (  ) Эх, пропал запал.
Цитата Race (  ) Любой способ при помощи которого возможно построить прямую параллельную двум другим параллельным прямым, подходит для построения прямой принадлежащей тому же пучку прямых (обзовем прямые имеющие общую точку пересечения - пучком) что и 2 произвольных прямых, можно применять и в обратном направлении, любой способ позволяющий построить прямую принадлежащую пучку, позволяет построить прямую параллельную 2 параллельным прямым.Это обусловлено тем, что параллельные прямые можно рассматривать как пересекающиеся, но точка их пересечения бесконечно удалена. При таком допущении, все иные законы Эвклидовой геометрии продолжают выполняться.
Пять раз перечитал, но всё равно чего-то не понял :O_o:
С шестого раза дошло 
Сообщение отредактировал erudite-man - Ср, 20.09.17, 21:57 |
| |
| |
| Race | Дата: Чт, 22.02.18, 21:28 | Сообщение # 9 |

Просветленный  Сообщений: 459
| Метод "трапеции"
Если кому то интересно, я могу выложить еще 3 метода для построения прямых параллельных 2 заданным, либо проходящих через произвольную точку и пучок.
Только построения будут не такими красивыми, так как в геогебре у меня не очень получается, буду чертить в автокаде.Добавлено (22.02.2018, 21:28)
---------------------------------------------
Можно полегче.
5. На плоскости даны 2 точки А и В. Между ними забит гвоздь, это значит что построить прямую АВ нет возможности. За минимальное кол-во действий построить некоторую точку С принадлежащую прямой АВ.
6. Можно ли на плоскости расположить три е точки А, В и С таким образом, что бы выполнялась возможность построения прямой ED параллельной АВ. Если можно, то каким образом?
Сообщение отредактировал Race - Чт, 21.09.17, 07:38 |
| |
| |


















 вы абсолютно правы! Если Вам интересно, командуйте, буду еще задачки выкладывать)
вы абсолютно правы! Если Вам интересно, командуйте, буду еще задачки выкладывать)
 )
)


