|
Построим касательные
|
|
| Race | Дата: Чт, 11.05.17, 14:47 | Сообщение # 1 |
Просветленный  Сообщений: 459
| Дана произвольная окружность и лежащая вне её точка А.
Требуется построить касательные из т. А к окружности используя только линейку.
|
| |
| |
| MrCredo | Дата: Чт, 11.05.17, 17:10 | Сообщение # 2 |
Мудрец  Сообщений: 619
| Готово 
|
| |
| |
| Race | Дата: Чт, 11.05.17, 18:17 | Сообщение # 3 |
Просветленный Сообщений: 459
| Как вариант конечно.... Но вы могли ошибиться на пару микрон)))
|
| |
| |
| zhekas | Дата: Чт, 11.05.17, 21:32 | Сообщение # 4 |
Гуру  Сообщений: 166
Совы: 6 
| 
|
| |
| |
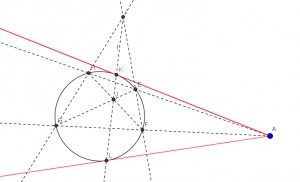
| Race | Дата: Пт, 12.05.17, 10:53 | Сообщение # 5 |
Просветленный Сообщений: 459
| zhekas,  Вы абсолютно правы.
А эту задачу не посмотрите? А то никто не хочет решать.
Сообщение отредактировал Race - Пт, 12.05.17, 10:57 |
| |
| |
| zhekas | Дата: Пт, 12.05.17, 14:55 | Сообщение # 6 |
Гуру Сообщений: 166
Совы: 6
| Ну с фиксированной точкой А проблем нет. Строим на луче AN Строим отрезок AM = 3AN. Дальше строим параллелограм ABMC. Собственно вот и получили треугольник ABC
|
| |
| |
| Race | Дата: Пт, 12.05.17, 15:20 | Сообщение # 7 |
Просветленный Сообщений: 459
| Да, с доступной т. А, легко, сразу получаем т. основания медианы Ma, дальше можно и через параллелограмм и через свойство трапеции, да и многими другими способами построить.
Вот с недоступной т. А интереснее)
|
| |
| |
| zhekas | Дата: Сб, 13.05.17, 00:19 | Сообщение # 8 |
Гуру Сообщений: 166
Совы: 6
| 
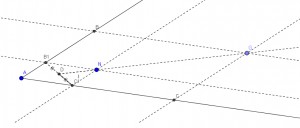
Из точки N проводим прямые параллельные лучам угла. Они (прямые) пересекаются с лучами в точках B1 и C1. Точка D - середина отрезка B1C1. Отрезок DG равен пяти отрезкам DN. Из точки G проводим прямые параллельные лучам угла. И вот они искомые B и C
|
| |
| |
| Race | Дата: Сб, 13.05.17, 08:57 | Сообщение # 9 |
Просветленный Сообщений: 459
| Награда будет через немного позже, пока не дает вручить.
Для построения отрезка который опирается на стороны угла и точкой разделен в определенной пропорции, достаточно провести линию параллельную одной из сторон угла и удаленную от точки на n*a, где a расстояние от точки до стороны, а n-пропорция согласно которой отрезок разделен заданной точкой.
То есть, если итоговые отрезки имеют отношение 1 к 1му n=1 (параллелограмм из 1 варианта задачи), в данном случае 2 к 1му.
Точка пересечения построенной параллельной прямой с второй стороной угла и будет искомой.
Геометрически доказывается так же кк с параллелограммом, к примеру если задана точка и нам необходимо вписать отрезок опирающийся на стороны угла, при этом разделенный точкой на 2 части в пропорции 1 к 2 (медианы) то имеем очевидное построение:
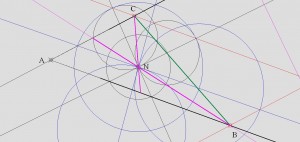
На рисунке 2 мы вписываем в угол отрезок разбитый точкой N в соотношении 1 к 1, тут меньше построений и все выглядит более наглядно.
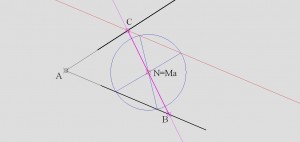
Соответственно на Вашем построении, будет иметь место соотношение:
B1B=2C1N
C1C=2B1N
Сообщение отредактировал Race - Сб, 13.05.17, 09:12 |
| |
| |
| Sezam | Дата: Чт, 13.07.17, 12:25 | Сообщение # 10 |
Знаток  Сообщений: 20
Совы: 0
| если угол наклона 45% то возможно ответ и правильный Добавлено (13.07.2017, 12:25)
---------------------------------------------
хотя это тоже зависит от построения
|
| |
| |
