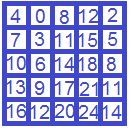
А что в этом удивительного? Давайте, представим себе, что все числа в каждой строчке (или столбце) одинаковые, тогда совершенно очевидно,что следуя условию, мы будем получать одну и ту же сумму. Например:
55555
77777
88888
11 11 11 11 11
25 25 25 25 25
Нам остаётся только сформировать "закон сохранения суммы" при внесении изменений в эту матрицу. Собственно у меня нет никаких сомнений, что в математике он давно уже сформулирован. Но так как я совершенно не помню этот ее раздел, попробую сообразить сам.
Сразу можно отметить симметрию между столбцами и строками, т.е. если одну группу чисел в строке (или столбце мы уменьшаем, то оставшуюся должны на столько же увеличить.
65..645
76..687
...
656
878
767
7... Но не сегодня)
Тем не менее, у меня нет сомнений, что ответ на заданный вопрос"потому что его так составили"
Добавлено (29.01.2018, 23:57)
---------------------------------------------
Пожалуй, dima-dirushka, пошел более прямым путем. Действительно,что мы видим? Каждый столбец сформирован так, что A(i+1)=A(i)+3.
Т.к. согласно условию, мы обязаны перебрать все столбцы (и строки) ровно по 1 разу,какую бы"дорожку" мы не выбрали, в итоге мы получим сумму элементов 1й строки + 3*(1+2+3+4)=26+30=56Добавлено (30.01.2018, 00:12)
---------------------------------------------
Собственно, тождественная сумма получается всякий раз,когда элементы одной строки отличаются от парных по столбцу элементов смежной строки на одну и ту же константу.