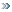Формула расчета нулей для реперных точек, коими являются 5
5n=5n-1+5n-2+....+51+50
Соответственно кол-во нулей A для n! можно посчитать как:
A=q(5k+5k-1+5k-2...+51+50)+w(5k-1+5k-2...+51+50)+e(5k-2+5k-3...+51+50)+...+t*50
Разбив для этого n, как:
n=q*5k+1+w*5k+e*5k-1+...t*51+R
Для любого R<5.Где коэффициенты q, w, e, t и так далее Є[1;4]
То есть, берем n=10161=3*55+1*54+1*53+1*52+2*51+1*50
Пусть A -кол-во нулей в конце, имеем
A=3*(54+53+52+51+50)+1*(53+52+51+50)+1*(52+51+50)+1*(51+50)+2*50= 3*781+1*156+1*31+1*6+2*1=2538 нулей.Добавлено (01.11.2016, 13:50)
---------------------------------------------
Определим m. Для этого рассмотрим все числа принадлежащие к натуральным Є N. тогда m, это числа которые выкалываются из N. выкалывание происходит когда n достигает значения 25. выкалывается 1 цифра.
Математически можно описать как при достижении n значения 5k происходит выкалывание k-1 цифры из n. Запишем в виде ряда:
0,1,2,3,4,5,6,7,8,9,10, 11,12,13,14,15,16, 17,18,19,20,21,22,23,24, 25, 26, 27, 28, 29, 30, 31,32,33,34,35, 36,
Прослеживается зкономерность, что не выколотые числа всегда идут по 5, потом 6 число выкалывается, можно организовать их в группу В, после 5 В выкалывается уже 2 числа, объеденим их в группу С то есть, получим:
В=5+1, С=5B+2, D=5C+3, E=5D+4 и так далее.
Числа m можно получить подставив в это уравнение.
Обязательно считаем что 1 число это 0!
{5, (+6) 11, (+6) 17, (+6) 23}=1*B
6*1*5-1 (-1 появилось так как 0 мы учитываем)
(+6) 29, (+1) 30,36,42,48,54,60, 61 и так далее, главное помнить, что каждая группа даст увелечение на 1 прокол, и соблюдать правильность формирования групп, С состоит из В, D состоит из С.