На мой взгляд апория "Ахиллес и черепаха" скорее софизм а не апория.
Апория по определению это логически верное рассуждение
Софизм по определения ложное суждение изночально создающее впечатление истинного рассуждения.
Все рассуждения включая вывод апории "Ахиллес и черепаха" согласно определению апории должны быть логически верными, тесть вывод данной апории может быть доказан исходя из ее рассуждений.
Однако при попытке доказательства вывода,-"Ахиллес никогда не догонит черепаху" ,- доказывается более слабое утверждение.
Пусть Ахиллес и черепаха стартуют в момент времени t
0, момент времени в который Ахиллес достиг точки старта черепахи обозначим t
1, момент времени в который Ахиллес оказался в точке в которой черепаха была в момент t
1 обозначим t
2и т.д, что можно записать следующим образом:
Верхняя строчка интервал времени, нижняя величина интервала
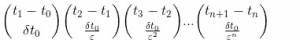
Вспомним что геометрическая прогрессия имеет вид:
а
n=а
0q
nСумма нескольких членов геометрической прогрессии вычесляется как
а
0+а
1+а
2+....+а
n-1=(a
0-a
n)/(1-q)
В нашем случае а
0=δt
0;q=1/ε
Тогда формулу суммы первых n членов можно представить в виде:
(δt
0-δt
0/ε
n)/(1-(1/ε))=(δt
0-δt
0/ε
n)•ε/(ε-1)
Вполне очевидно что величина (δt
0-δt
0/ε
n) при любых n строго меньше δt
0 поэтому(δt
0-δt
0/ε
n)<δt
0•ε/(ε-1)
Таким образом декларируемый в апории тезис ложен, а логически верно более слабое утверждение,-После старта в течении интервала времени δt
0•ε/(ε-1) Ахиллес не догонит черепаху.
Таким образом рассуждения апории имеют ложное утверждение, что противоречит определению апории, и подподает под определение софизма.
Если утверждение "Ахиллес никогда не догонит черепаху" ложное, значит верно обратное,- Ахиллес догонит черепаху за конечное время.
Данное утверждение просто доказать используя довольно элементарные рассуждения.
Будем спользовать условия данной задачи (скорость черепахи 1 м/мин, скорость Ахиллеса 500 м/мин) и принимем расстояние между Ахиллесом и черепахой в 250км.
Расстояние между Ахиллесом и черепахой, Ахиллес преодалеет за 500 минут, следующий этап займёт 1 минуту, следующий за 0,002 минуты, таким образом получаем последовательность интервалов
500,500/500,500/500²,...,500/500ⁿ....
Таким образом сумма всех членов данной последовательности будет моментом времени в который Ахиллес догонит черепаху, если конечно ряд сходится.
В том что ряд
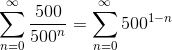
сходится легко понять начиная складывать последовательно 2,3,4,5 первых членов.
Вспоминая опять о геометрической прогрессии из школьного курса известно что:
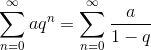
Поэтому Ахиллес догонит черепаху через
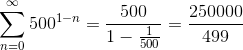
минут.
Таким образом если расстояние перед стартом между Ахиллесом и черепахой S, скорость Ахиллеса V
a, скорость черепахи V
ч, то Ахиллес настигает черепаху через t=S/(V
a-V
ч)

















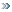









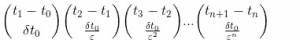
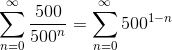 сходится легко понять начиная складывать последовательно 2,3,4,5 первых членов.
сходится легко понять начиная складывать последовательно 2,3,4,5 первых членов.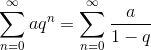
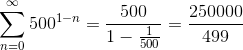 минут.
минут.
