Интересно. Правда ничего не понятно так как Ваши рисунки не грузятся.
Для решения необходимо помнить всего одну теорему из школьной программы, точнее одну из её интерпритаций. Теорема Менелая.
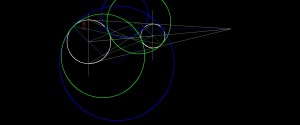
1. Проводим секущую из центра гомотетии, таким образом что бы она проходила через заданную точку.
2. Каждая из секущих даст 4 точки пересечения с двумя окружностями, это и будут возможные точки касания построенной окружности.
3. Через эти точки и центры заданных окружностей проводим прямые, находим 4 центра, строим окружности. На секущей проведенной их внешнего центра гомотетии точки касания будут 1-4 (слева направо) и 2-3, для внутреннего центра гомотетии 1-3 и 2-4 в силу того что окружность будет зеркально отображена.
4. Доказать можно самостоятельно, либо рассмотреть теорему Менелая, в задачах на построение окружности касательной к точке и двум окружностям. В этом случае она как раз принимает удобную нам форму.