|
Построить окружность.
|
|
| Race | Дата: Ср, 26.10.16, 11:37 | Сообщение # 1 |

Просветленный  Сообщений: 459
| Имеем две произвольные не пересекающиеся и не находящиеся одна внутри второй окружности.
Требуется построить окружность касающуюся к двум окружностям и проходящую через произвольно выбранную, принадлежащую одной из окружностей точку.
Пробудим в эрудитах любовь к геометрии) 
Сообщение отредактировал Race - Ср, 26.10.16, 11:40 |
| |
| |
|
| Race | Дата: Сб, 29.10.16, 21:41 | Сообщение # 3 |

Просветленный  Сообщений: 459
| Совершенно верно. Вы первый кто на этом сайте, при мне применил инверсию.
А если без инверсии? Ведь задача Аполлония изначально без нее решалась?
Награду отправляю, одно НО, методом инверсии к этой точке можно построить 2 окружности которые будут касаться исходной точки.
Ваш подход несколько нестандартен  Награду отправляю. Награду отправляю.
|
| |
| |
| zhekas | Дата: Сб, 29.10.16, 21:57 | Сообщение # 4 |

Гуру  Сообщений: 166
Совы: 6 
| Цитата zhekas (  ) НО, методом инверсии к этой точке можно построить 2 окружности которые будут касаться исходной точки. |
| |
| |
| Race | Дата: Сб, 29.10.16, 22:00 | Сообщение # 5 |

Просветленный  Сообщений: 459
| Цитата zhekas (  ) Ну логично. Ведь к окружности (s) можно построить две касательных.  Без инверсии попробуете решить? Без инверсии попробуете решить?
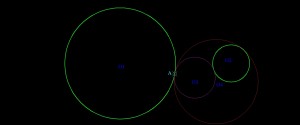
|
| |
| |
| zhekas | Дата: Пн, 31.10.16, 22:09 | Сообщение # 6 |

Гуру  Сообщений: 166
Совы: 6 
| Цитата Race (  ) А если без инверсии?
Решение в соседней теме.
|
| |
| |
| Race | Дата: Пн, 31.10.16, 22:13 | Сообщение # 7 |

Просветленный  Сообщений: 459
| Я уже прочитал спасибо.
|
| |
| |
| zhekas | Дата: Пн, 31.10.16, 22:13 | Сообщение # 8 |

Гуру  Сообщений: 166
Совы: 6 
| Чем чертишь?
|
| |
| |
| Race | Дата: Пн, 31.10.16, 22:17 | Сообщение # 9 |

Просветленный  Сообщений: 459
| Я с телефона сейчас, потому не могу цитировать, черчу по старинке автокадом.
|
| |
| |























 Награду отправляю.
Награду отправляю.


