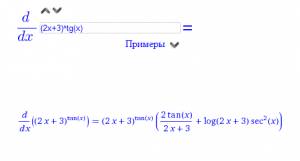
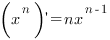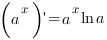Мало кто знает, что ...
Скорость передвижения морского конька 0.01 км/ч
| Задачи | Иллюзии | Загадки | Хочу Знать! | Твесты | Форум Эрудитов |
|
| Форум Эрудитов » Логические задачи и головоломки » Скорая помощь » Решенные задачи » математика (sml[ok]) |
| математика | |||||||||
| |||||||||
|
| |||
| |||
| Интересная информация | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Последние задачи | Сообщество эрудитов ВКонтакте | Рейтинг сообщений | Совиный рейтинг | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||