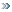|
Отношение порядка
|
|
| Kreativshik | Дата: Пт, 10.04.15, 21:19 | Сообщение # 1 |

Гений  Сообщений: 2472
| Сколько делителей у следующего числа:
77777x•88888y•99999z•66!
?
|
| |
| |
| Kreativshik | Дата: Пт, 10.04.15, 21:56 | Сообщение # 2 |

Гений  Сообщений: 2472
| Если возникнут трудности, скажите, я подскажу.
|
| |
| |
| никник | Дата: Пт, 10.04.15, 22:54 | Сообщение # 3 |

Высший разум  Сообщений: 2770
| 77777x•88888y•99999z•66!
7^x*11111^(x+y+z)*2^3y*3^2z*66!
66!=1*2^33*3^22*5^13*7^9*11^6*13^5*17^3*19^3*23^2*29^2*31^2*37^2*41*43*47*53*59*61/109сомнож.
11111=271*41 /2*(х+y+z)сомнож
Итого имеем: 109+4x+5y+4z простых сомножителей. А их сочетаний, видимо, будет ((109+4x+5y+4z)-1)!
(?)
Сообщение отредактировал никник - Пт, 10.04.15, 23:05 |
| |
| |
| Kreativshik | Дата: Пт, 10.04.15, 23:02 | Сообщение # 4 |

Гений  Сообщений: 2472
| 
|
| |
| |
| никник | Дата: Пт, 10.04.15, 23:07 | Сообщение # 5 |

Высший разум  Сообщений: 2770
| От самого начала неверно? или дайте хоть цитату с какого момента.
|
| |
| |
| Kreativshik | Дата: Пт, 10.04.15, 23:12 | Сообщение # 6 |

Гений  Сообщений: 2472
| Цитата никник (  ) с какого момента.
Сразу после этогоЦитата никник (  ) 77777x•88888y•99999z•66!
|
| |
| |
| Kreativshik | Дата: Пт, 10.04.15, 23:54 | Сообщение # 7 |

Гений  Сообщений: 2472
| никник, давайте рассмотрим более простую но аналогичную задачу:
Сколько делителей у числа 13х•23у•47z
|
| |
| |
| никник | Дата: Сб, 11.04.15, 02:37 | Сообщение # 8 |

Высший разум  Сообщений: 2770
| (1+x)(1+y)(1+z), мне кажется
|
| |
| |
| никник | Дата: Сб, 11.04.15, 03:15 | Сообщение # 9 |

Высший разум  Сообщений: 2770
| Тогда,вроде, так:
1*2^(33+3y)*3^(22+2z)*5^13*7^(9+x)*11^6*13^5*17^3*19^3*23^2*29^2*31^2*37^2*41^(1+x+y+z)*43*47*53*59*61*271^(x+y+z)
(1+1)^5*(33+3y+1)*(23+2z)*14*(10+x)*7*6*4*4*3^4*(2+x+y+z)*(1+x+y+z)=
2048*49*243*(34+3y)(23+2z)*(10+x)(2+x+y+z)*(1+x+y+z)=24385536*(34+3y)(23+2z)*(10+x)(2+x+y+z)*(1+x+y+z)
|
| |
| |
| zhekas | Дата: Сб, 11.04.15, 08:52 | Сообщение # 10 |

Гуру  Сообщений: 166
Совы: 6 
| Цитата никник (  ) Тогда,вроде, так:
1*2^(33+3y)*3^(22+2z)*5^13*7^(9+x)
у 66! не 33 степени двойки. Потому что некоторые множители из 66! делятся не только на 2, но и на 4 и на 8 и т.д. Точно так же с 3,5,7.
Сообщение отредактировал zhekas - Сб, 11.04.15, 08:52 |
| |
| |