|
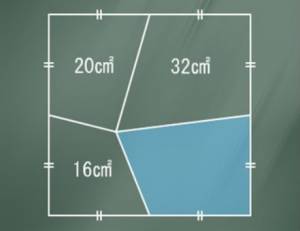
Площадь фигуры
|
|
|
| marutand | Дата: Вт, 02.07.13, 16:04 | Сообщение # 2 |

Гуру  Сообщений: 331
| 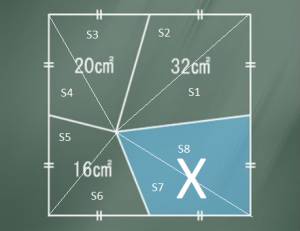
т.к если основания и соответствующие высоты треугольников равны то и их площади равны для полученных в результате дополнительных построений треугольников можно написать:
S2=S3;(1)
S4=S5;(2)
S6=S7;(3)
S8=S1;(4)
С другой стороны:
S1+S2=32;(6)
S3+S4=20;(7)
S5+S6=16;(8)
S7+S8=X ;(9)
Делая соответствующие постановки из 1-4 в 6-8 получим:
S1+S2=32;(10)
S2+S4=20;(11)
S4+S6=16;(12)
S6+S1=X;(13)
Далее поставив s2 из 10 в 11, а из полученного в результате уравнения S4 в 12 получим:
X=S1+S6=28;
Ответ: 28см2
|
| |
| |
|
| Гретхен | Дата: Вт, 02.07.13, 21:30 | Сообщение # 4 |

Гений  Сообщений: 1807
| Мне кажется, что должно быть еще как минимум одно решение, при всем моем уважении к решению marutand. Я попыталась что-то накроить и выкроить в доказательной базе, но, видимо, мне не хватает знаний. Но то решение, которое математически обосновывает интуитивное - ну вот должно быть, хоть ты тресни. Ростислав, не мог бы ты продублировать эту задачку еще раз, и в предисловии написать, что нужно решение, отличное от этого?
|
| |
| |
| marutand | Дата: Ср, 03.07.13, 17:10 | Сообщение # 5 |

Гуру  Сообщений: 331
| Гретхен спасибо, по моему вы интуитивно чувствуйте что суммы площадей противоположных четырёхугольников равны. Это и на самом деле так и является следствием равенств треугольников 1-4,
так что после них можно было просто и коротко написать:
- Т.к из 1-4 следует что суммы площадей противоположных четырёхугольников равны то 48=20+Х; Х=28;
Сообщение отредактировал marutand - Ср, 03.07.13, 17:12 |
| |
| |
|
| Гретхен | Дата: Ср, 03.07.13, 23:48 | Сообщение # 7 |

Гений  Сообщений: 1807
| .
Сообщение отредактировал Гретхен - Ср, 03.07.13, 23:49 |
| |
| |
| Гретхен | Дата: Чт, 04.07.13, 07:23 | Сообщение # 8 |

Гений  Сообщений: 1807
| Цитата (Гретхен) marutand, спасибо за ответ. Но я не уверена... Пока не понимаю, как можно доказательно привязать равенство площадей БОЛЬШИХ треугольников к площадям заявленных четырехугольников...
До меня дошло 
|
| |
| |
| Гретхен | Дата: Вс, 04.08.13, 10:45 | Сообщение # 9 |

Гений  Сообщений: 1807
| Цитата (Гретхен) Мне кажется, что должно быть еще как минимум одно решение ... решение, которое математически обосновывает интуитивное - ну вот должно быть ...
|
| |
| |
| nebo | Дата: Пн, 05.08.13, 11:39 | Сообщение # 10 |

Высший разум  Сообщений: 3639
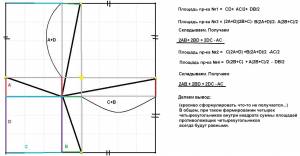
| У меня получилось ещё одно решение этой задачи.

Соединим середины сторон квадрата. Получим четыре абсолютно одинаковых
прямоугольных треугольника со сторонами а,а,b и квадрат, стороны которого
AC=CB=BD=AD=b. Эту сторону b примем за основание в каждом из четырёх,
не равных по площади, треугольников, образовавшихся во вписанном квадрате.
Высоту в каждом из них обозначим h, тогда:
S1=1/2*b*h1, S2=1/2*b*h2, S3=1/2*b*h3, S4=1/2*b*h4.
Из чертежа очевидно, что h1+h2=b и h3+h4=b. Отсюда:
S1+S2=1/2*b*h1+1/2*b*h2=1/2*b*(h1+h2)=1/2*b*b, также и
S3+S4=1/2*b*(h3+h4)=1/2*b*b, т.е.
S1+S2=S3+S4, а значит и (S+S1)+(S+S2)=(S+S3)+(S+S4) или
(S+S1)+20=16+32 S+S1=28см(квадратных).
|
| |
| |